
En el contexto peruano, desde el Currículo Nacional de la Educación Básica (Ministerio de Educación, 2016) se estipula en el perfil de egreso la importancia de que los estudiantes sean capaces de indagar sobre el mundo que les rodea, así como de asumir una postura crítica con respecto a una temática determinada. De la misma manera, la Organización del Bachillerato Internacional (2025) con un modelo educativo distinto al peruano, señala en su misión, formar educandos curiosos por el entorno que le rodea con la finalidad de desarrollar habilidades investigativas. Al respecto, queda expuesto que la investigación es un requerimiento que los modelos educativos quieren lograr en los alumnos que forman parte de ellos.
No obstante, ¿Qué ocurre con los estudiantes cuando ingresan a la educación superior? Amézquita et al. (2020) y Díaz-León (2023) presentan que la realidad de la investigación de los estudiantes universitarios es compleja y desafiante, ya que se ve influida por una escasa formación metodológica y una cultura investigativa aún en construcción. Esta situación guarda relación con lo que ocurre en la educación secundaria, donde la investigación suele abordarse de forma superficial o como un requisito académico, sin una orientación clara ni un propósito formativo sólido (Córdova et al., 2021). En ambos niveles, persisten dificultades para vincular la investigación con el contexto del estudiante y fomentar una mirada crítica y reflexiva sobre su entorno, lo que evidencia la necesidad de fortalecer desde etapas tempranas una cultura investigativa significativa y situada.
En este marco, la modelización matemática se posiciona como un proceso que pueda contribuir al desarrollo de habilidades investigativas en los estudiantes, así como que puedan hacer con un contexto más cercano al de ellos, partiendo de sus intereses. Pero ¿Qué es la modelización matemática? En términos generales, puede definirse como un proceso que establece relaciones entre conceptos matemáticos y elementos del mundo real con el propósito de analizar, comprender o predecir fenómenos concretos (Álvarez y Patagua, 2018; Búa et al., 2015; Cervantes, 2015). Este enfoque permite que las matemáticas trasciendan los ejercicios abstractos para convertirse en una herramienta útil para interpretar situaciones diversas, desde contextos cotidianos hasta problemas científicos o sociales complejos, es decir, la investigación.
Figura 1
Fases de la modelación matemática
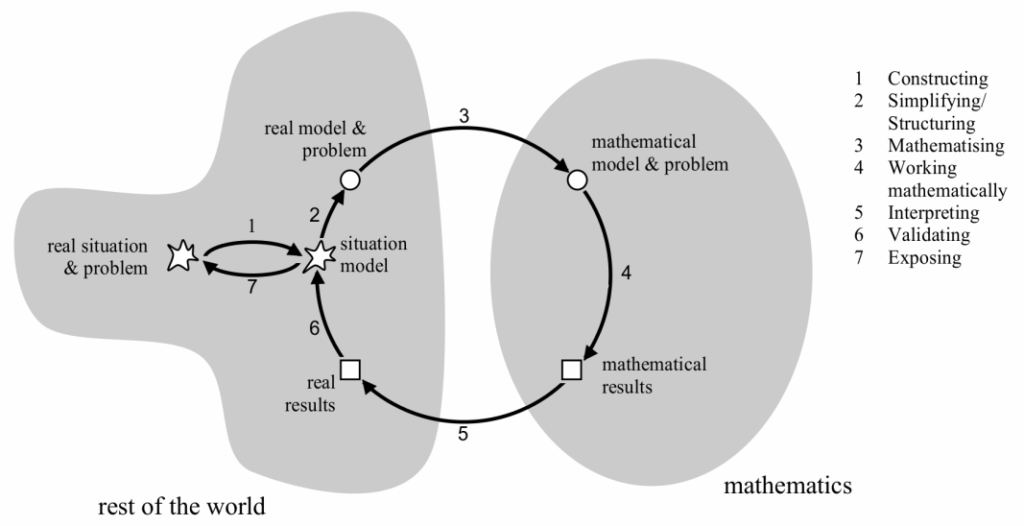
Nota. El esquema presenta la secuencia para trabajar con la modelación matemática. Tomado de Búa et al. (2015).
Tal cual presenta la figura 1, la modelización matemática parte de dos conjuntos: el mundo real y la matemática. Como se visualiza, se parte desde una problemática la realidad para ir escalando los demás pasos que permitirán estructurar, dejando de lado aspectos innecesarios debido a la investigación que se hace, el modelo matemático que se realizará para atender a las necesidades del problema encontrado y reflexionar sobre el proceso hecho. Por lo tanto, esta manera de trabajar con el entorno del estudiante, ofrece a las matemática una forma de comprenderlo desde la práctica e investigación
En ese sentido Gallart et al. (2019) sugiere que esta forma de hacer matemática favorece al desarrollo de aprendizajes duraderos al trabajar con la realidad, ya que permite a los estudiantes establecer conexiones significativas entre los contenidos escolares y su entorno. Al enfrentar situaciones que requieren interpretar, representar y resolver problemas auténticos, los estudiantes aplican conocimientos matemáticos y desarrollan habilidades de pensamiento crítico, así como de toma de decisiones. En este sentido, la matemática deja de percibirse como un conjunto aislado de procedimientos para convertirse en una herramienta viva y funcional para comprender el mundo.
Asimismo, en la línea de comprender el mundo, la modelización matemática ofrece oportunidades a los estudiantes de explorar fenómenos complejos desde una perspectiva analítica, formular conjeturas, tomar decisiones fundamentadas y argumentar sus ideas con base en datos y representaciones matemáticas (Rei y Gioda, 2020). Esta práctica fortalece su competencia matemática y promueve una actitud reflexiva frente a los problemas de su contexto, brindándoles herramientas para participar activamente en la sociedad. De este modo, la modelización se convierte en un puente entre la escuela y la vida real, donde aprender matemáticas implica también desarrollar una mirada crítica sobre la realidad. No se trata únicamente de repetir que ‘la matemática está en todo’, sino de profundizar en las razones de su presencia, comprendiendo cómo y por qué interviene en los distintos aspectos de la vida cotidiana, social y cultural.
Figura 2
La realidad de la frase: “La matemática está en todo”

Nota. Posible situación cotidiana cuando se habla del sentido de las matemáticas en la vida de los estudiantes. Tomado de Villa-Ochoa et al. (2009).
Haciendo referencia a la figura 2, si bien es cierto que existe un discurso común al responder la pregunta ‘¿para qué sirven las matemáticas?’, el cual suele reproducirse de forma mecánica como se muestra en la imagen, es a través de la modelización matemática y la investigación que los estudiantes pueden realmente comprender ese discurso. Al sumergirse en estos procesos, tienen la oportunidad de descubrir cómo la matemática configura su realidad, permitiéndoles construir significados propios y relevantes.
En síntesis, enseñar matemáticas no debería limitarse a la transmisión de algoritmos y procedimientos, sino que implica también generar experiencias donde el estudiante pueda vivenciar la matemática, apropiarse de ella y reconocer su utilidad en la comprensión del mundo que lo rodea. Porque cuando las y los estudiantes descubren el sentido de lo que hacen, las matemáticas dejan de ser ajenas y se convierten en parte de su propia historia. Así, la investigación y la modelización matemática ofrecen oportunidades valiosas para enriquecer el aprendizaje, pues permiten que los estudiantes se involucren activamente en la construcción de conocimientos a partir de situaciones reales y significativas.
Anexo un ejemplo del producto generado durante el proceso de modelización matemática, desarrollado en el curso Conexiones entre la Matemática, Física y Química, dictado en el ciclo 2024-2 por el Dr. Mihály Martínez Miraval, especialista en Matemática Educativa. En dicho producto apliqué el modelo SIR para analizar la propagación del COVID-19 en el distrito de Jesús María el año 2020, tomando de base información del Ministerio de Salud y del INEGI, a través de GeoGebra. Cabe resaltar que es una simulación, los datos no son tan exactos (Applet: https://www.geogebra.org/m/j7yjawvb)
Figura 3
Gráfica del Modelo SIR que simula la evaluación de la Covid-19 en el distrito de Jesús María
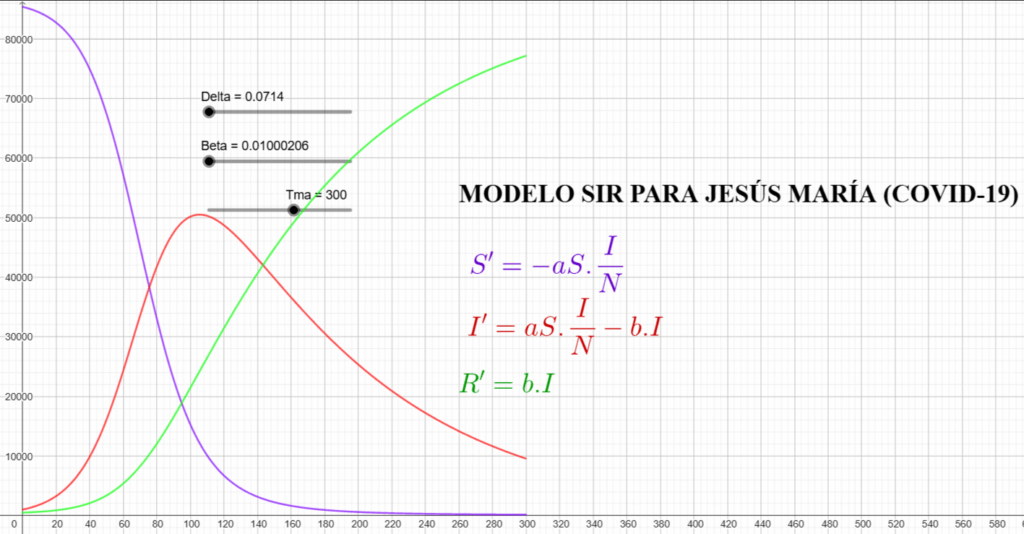
Nota. Elaboración propia.
La figura 3 muestra una simulación del modelo SIR aplicada al distrito de Jesús María durante la pandemia de COVID-19. Este modelo epidemiológico divide a la población en tres grupos: susceptibles (S), infectados (I) y recuperados (R). En la gráfica, la curva morada representa la cantidad de personas susceptibles, que disminuye a medida que el virus se propaga. La curva roja muestra la evolución de los infectados, que aumenta inicialmente hasta alcanzar un pico y luego desciende. Finalmente, la curva verde indica a las personas recuperadas, cuyo número crece progresivamente con el tiempo. Las ecuaciones diferenciales a la derecha describen el comportamiento del modelo, donde la tasa de infección está representada por el parámetro a (asociado a Beta = 0.01000206), y la tasa de recuperación por b (asociado a Delta = 0.0714). Además, se ha fijado un tiempo máximo de análisis (Tma = 300) para observar la evolución completa del brote.
Nota elaborada por:

Cesar Antonio Palacios Poma
Estudiante de educación secundaria con especialidad en Matemáticas
Referencias:
Álvarez, V. V., & Patagua, I. A. (2018). Modelización matemática: Análisis de una experiencia aúlica en la secundaria. Acta Latinoamericana de Matemática Educativa, 31(1), 534-542. https://funes.uniandes.edu.co/wp-content/uploads/tainacan-items/32454/1151718/Alvarez2018Modelizacion.pdf
Amésquita, M., Ávila, D., Condori, A. y García, M. (2020). La investigación científica en la universidad peruana. Journal of the Academy, (3), 32-39. https://pdfs.semanticscholar.org/cf27/ac0db5c1f6ebed45410c83dccf62a263f90f.pdf
Búa, J. B., Fernández, T. y Salinas, M. (2015). Una modelización matemática como medio de detección de obstáculos y dificultades de los alumnos sobre el concepto de función: alargamiento de un muelle sometido a un peso. Educación matemática, 27(1), 91-122. https://funes.uniandes.edu.co/funes-documentos/una-modelizacion-matematica-como-medio-de-deteccion-de-obstaculos-y-dificultades-de-los-alumnos-sobre-el-concepto-de-funcion-alargamiento-de-un-muelle-sometido-a-un-peso/
Cervantes, L. (2015). Consideraciones sobre la modelización matemática. En L. Cervantes Gómez (Coord.), Modelización matemática: Principios y aplicaciones (pp. 1–10). Benemérita Universidad Autónoma de Puebla. http://matema.ujaen.es/jnavas/web_modelos_empresa/archivos/materiales%20complementarios/texto%20modelos%20puebla.pdf
Diaz-León, I. (2023). La realidad de la investigación universitaria en el Perú: el rol de los docentes y estudiantes. Spirat. Revista Académica de Docencia y Gestión Universitaria, 1(2), 61-63. https://revistas.upch.edu.pe/index.php/Spirat/article/view/4442
Gallart, C., Ferrando, I. y García, L.(2019). Modelización matemática en la educación secundaria: manual de uso. Modelling in Science Education and Learning, 12(1), 71–86. https://doi.org/10.4995/msel.2019.10955
Ministerio de Educación. (2016). Currículo Nacional de la Educación Básica [Archivo PDF]. https://www.minedu.gob.pe/curriculo/pdf/curriculo-nacional-de-la-educacion-basica.pdf
Organización del Bachillerato Internacional. (2025). About the International Baccalaureate (IB). Bachillerato Internacional. https://www.ibo.org/about-the-ib/
Reid, M. E., & Gioda, R. B. (2020). Modelización Matemática en la Educación Secundaria. UNIÓN-REVISTA IBEROAMERICANA DE EDUCACIÓN MATEMÁTICA, 16(59), 275-292. https://funes.uniandes.edu.co/wp-content/uploads/tainacan-items/32454/1190018/Reid2020Modelizaci25C325B3n.pdf
Villa-Ochoa, J., Quintero, C., Arboleda, M., Castaño, J. y Ocampo, D. (2009). Sentido de realidad y modelación matemática: el caso de Alberto. Alexandria: Revista de Educação em Ciência e Tecnologia, 2(2), 159-180. https://dialnet.unirioja.es/descarga/articulo/6170694.pdf